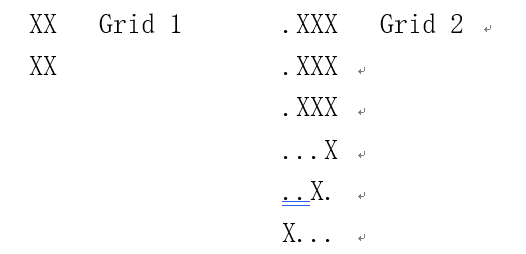有的题还没写完)咕咕咕))
这学期写算法2的思路并不都很详细,不过如果有想交流的也可以评论区或者私信,学校oj的题大多比较简单,这里的所有代码或许只保证通过学校的弱测试数据,因为其他地方OJ我还没有试过。
猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半另加一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子。
输入
输入第一行为正整数n,为测试数据组数。后面n行为测试数据,每组测试数据包括两个整数m,k,分别表示第m(m>1)天后剩余的桃子数k(k>=0)。
输出
输出猴子第一天摘的桃子数,每组数据占一行。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<bits/stdc++.h>
using namespace std ;
int main () {
int n ; cin >> n ;
while ( n -- ) {
int m , k ; cin >> m >> k ;
int sum = k ;
for ( int i = 0 ; i < m - 1 ; i ++ ) {
sum ++ ;
sum *= 2 ;
}
cout << sum << endl ;
}
return 0 ;
}
输入两个正整数,求其最大公约数。
数论中有一个求最大公约数的算法称为辗转相除法,又称欧几里德算法。其基本思想及执行过程为(设m为两正整数中较大者,n为较小者):
(1)令u=m,v=n;
(2)取u对v的余数,即r=u%v,如果r的值为0,则此时v的值就是m和n的最大公约数,否则执行第(3)步;
(3)u=v,v=r,即u的值为v的值,而v的值为余数r。并转向第(2)步。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括两个正整数m和n。
输出
n行,每行输出对应一个输入。输出应是一个正整数,为m和n的最大公约数。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<bits/stdc++.h>
using namespace std ;
int main () {
int t ; cin >> t ;
while ( t -- ) {
int m , n ; cin >> m >> n ;
int yu = m % n ;
while ( yu ) {
m = n ; n = yu ;
yu = m % n ;
}
cout << n << endl ;
}
return 0 ;
}
有一个汉诺塔,塔内有A,B,C三个柱子。起初,A柱上有n个盘子,依次由大到小、从下往上堆放,要求将它们全部移到C柱上;在移动过程中可以利用B柱,但每次只能移到一个盘子,且必须使三个柱子上始终保持大盘在下,小盘在上的状态。要求编程输出移动的步骤。
输入
输入文件中包含多行,每行为一个整数n,代表初始A柱子上的盘子的个数。
输出
对输入文件中的每个整数n列出具体的汉诺塔移动步骤。两组输出之间有一空行。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C
A-->C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std ;
void hanoi ( int n , int from , int to ) {
if ( n == 0 ) return ; // 全部移完,终止递归
// 把from位置上的上面的n-1个移到不是from也不是to的位置
hanoi ( n - 1 , from , ( 3 - from - to ));
// 移动最底下的最大的那个,并输出记录
cout << char ( from + 'A' ) << "-->" << char ( to + 'A' ) << endl ;
// 把之前移走的n-1个移到to位置
hanoi ( n - 1 , ( 3 - from - to ), to );
}
int main () {
int n ;
while ( cin >> n ) {
hanoi ( n , 0 , 2 );
cout << " \n " ;
}
return 0 ;
}
菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1,接下来每个数都等于前面2个数之和。给出一个正整数a,要求菲波那契数列中第a个数是多少。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a(1 <= a <= 20)。
输出
输出有n行,每行输出对应一个输入。输出应是一个正整数,为菲波那契数列中第a个数的大小。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<bits/stdc++.h>
using namespace std ;
int fib ( int n ) {
if ( n == 1 || n == 2 ) return 1 ;
return fib ( n - 1 ) + fib ( n - 2 );
}
int main () {
int t ; cin >> t ;
while ( t -- ) {
int a ; cin >> a ;
cout << fib ( a ) << endl ;
}
return 0 ;
}
定义另外一个Fibonacci数列:F(0)=7,F(1)=11,F(n)=F(n-1)+F(n-2),(n≥2)。
输入
输入文件中包含多行,每行为一个整数n,n<1000000。
输出
对输入文件中的每个整数n,如果F(n)能被3整除,输出yes,否则输出no。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
#include<bits/stdc++.h>
using namespace std ;
int main () {
long long na ;
while ( cin >> na ) {
if ( na % 8 == 2 || na % 8 == 6 ) cout << "yes \n " ;
else cout << "no \n " ;
}
return 0 ;
}
分形是存在“自相似”的一个物体或一种量,从某种技术角度来说,这种“自相似”是全方位的。
盒形分形定义如下:
度数为1的分形很简单,为:
X
度数为2的分形为:
X X
X
X X
如果用B(n-1)代表度数为n-1的盒形分形,则度数为n的盒形分形可以递归地定义为:
B(n-1) B(n-1)
B(n-1)
B(n-1) B(n-1)
你的任务是输出度数为n的盒形分形。
输入
输入文件包含多个测试数据,每个测试数据占一行,包含一个正整数n,n ≤ 7。输入文件的最后一行为-1,代表输入结束。
输出
对每个测试数据,用符号“X”表示输出盒形分形。在每个测试数据对应的输出之后输出一个短划线符号“-”,在每行的末尾不要输出任何多余的空格,否则得到的是“格式错误”的结果。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
X X
X
X X
-
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std ;
const int maxlen = pow ( 3 , 8 );
// string mp[maxlen];
char mp [ maxlen ][ maxlen ];
int xpos [ maxlen ];
void tocpyRec ( int deg , int tox , int toy , int fillblank ) {
int len = pow ( 3 , deg - 1 );
// 左上角标记
for ( int i = 0 ; i < len ; i ++ ) {
for ( int j = 0 ; j < len ; j ++ ) {
// cout << mp[i][j] << ":" << i << "-" << j << endl;
if ( fillblank )
mp [ tox * len + i ][ toy * len + j ] = ' ' ;
else
mp [ tox * len + i ][ toy * len + j ] = mp [ i ][ j ];
}
}
}
void fw ( int deg ) {
if ( deg > 1 ) {
fw ( deg - 1 );
}
for ( int i = 0 ; i < 3 ; i ++ ) {
for ( int j = 0 ; j < 3 ; j ++ ) {
if (( i + j ) % 2 == 0 && ( i || j )) {
// 有内容的块坐标
tocpyRec ( deg - 1 , i , j , 0 );
}
else if ( i || j ) {
tocpyRec ( deg - 1 , i , j , 1 );
}
}
}
}
int main () {
mp [ 0 ][ 0 ] = 'X' ;
int n ;
int flag = 0 ;
while ( cin >> n && n != - 1 ) {
if ( flag ) cout << "- \n " ;
flag = 1 ;
fw ( n );
int len = pow ( 3 , n - 1 );
for ( int i = 0 ; i < len ; i ++ )
for ( int j = 0 ; j < len ; j ++ )
if ( mp [ i ][ j ] == 'X' )
xpos [ i ] = j ;
for ( int i = 0 ; i < len ; i ++ ) {
for ( int j = 0 ; j <= xpos [ i ]; j ++ ) {
cout << mp [ i ][ j ];
}
cout << endl ;
}
}
return 0 ;
}
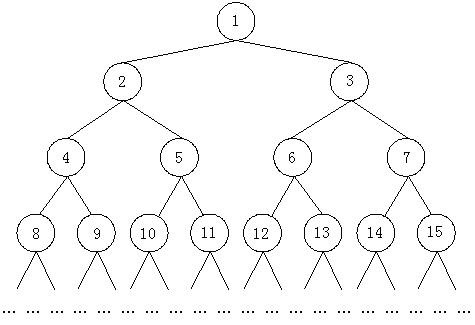
如图所示,由正整数1, 2, 3, …组成了一棵无限大的二叉树。从某一个结点到根结点(编号是1的结点)都有一条唯一的路径,比如从10到根结点的路径是(10, 5, 2, 1),从4到根结点的路径是(4, 2, 1),从根结点1到根结点的路径上只包含一个结点1,因此路径就是(1)。对于两个结点x和y,假设他们到根结点的路径分别是(x1, x2, … ,1)和(y1, y2, … ,1)(这里显然有x = x1,y = y1),那么必然存在两个正整数i和j,使得从xi 和 yj开始,有xi = yj , xi + 1 = yj + 1, xi + 2 = yj + 2,… 现在的问题就是,给定x和y,要求xi(也就是yj)。
输入
输入有多行,每行包括两个正整数x和y,这两个正整数都不大于1000。
输出
每行输出只有一个正整数xi。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std ;
const int N = 12 ;
int ax [ N ], ay [ N ];
int main () {
int x , y ;
// 找重合的路径
while ( cin >> x >> y ) {
int kx = 0 ;
while ( x ) {
ax [ kx ++ ] = x % 2 ;
x /= 2 ;
}
int ky = 0 ;
while ( y ) {
ay [ ky ++ ] = y % 2 ;
y /= 2 ;
}
int kmii = kx > ky ? ky : kx ;
int ans = 0 ;
for ( int i = 1 ; i <= kmii ; i ++ ) {
if ( ax [ kx - i ] == ay [ ky - i ]) {
ans <<= 1 ;
ans += ax [ kx - i ];
}
else break ;
}
cout << ans << endl ;
}
return 0 ;
}
波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的波兰表示法为+ 2 3。波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的波兰表示法为* + 2 3 4。本题求解波兰表达式的值,其中运算符包括+ - * /四个。
输入
输入第一行为一个整数n,然后是n行,每行为一组测试数据,其中运算符和运算数之间都用空格分隔,运算数是浮点数。
输出
输出n行,每行表达式的值,保留3位小数输出。
样例输入
1
2
1
* + 11.0 12.0 + 24.0 35.0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std ;
double dox () {
string st ; cin >> st ;
switch ( st [ 0 ])
{
case '+' :
return dox () + dox ();
case '-' :
return dox () - dox ();
case '/' :
return dox () / dox ();
case '*' :
return dox () * dox ();
default : break ;
}
return atof ( st . c_str ());
}
int main () {
int t ; cin >> t ;
while ( t -- ) {
cout << fixed << setprecision ( 3 ) << dox () << endl ;
}
return 0 ;
}
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法(用K表示)?注意:5,1,1和1,5,1 是同一种分法。
输入
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1 <= M,N <= 10。
输出
对输入的每组数据M和N,用一行输出相应的K。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std ;
const int N = 15 ;
int dp [ N ][ N ];
int divx ( int apl , int pla ) {
if ( apl == 0 || pla == 1 )
return dp [ apl ][ pla ] = 1 ;
if ( pla > apl )
return dp [ apl ][ pla ] = divx ( apl , apl );
return dp [ apl ][ pla ] = divx ( apl , pla - 1 ) + divx ( apl - pla , pla );
}
int main () {
int t ; cin >> t ;
int m , n ;
while ( t -- ) {
cin >> m >> n ;
cout << divx ( m , n ) << endl ;
}
return 0 ;
}
有5个人坐在一起,问第5个人多少岁?他说比第4个人大两岁。问第4个人的岁数,他说比第3个人大两岁。问第3个人的岁数,又说比第2个人大两岁。问第2个人的岁数,说比第1个人大两岁。最后问第1个人的岁数,他说是10岁。请问第5个人多少岁?
输入
输入有多行,每行3个整数,依次为m,n,k。m表示一共有几个人,n表示大的岁数,k表示第一个人的岁数。
输出
输出第m个人的岁数,每个一行。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<bits/stdc++.h>
using namespace std ;
int m , n , k ;
int age ( int ind ) {
if ( ind == 1 ) return k ;
return age ( ind - 1 ) + n ;
}
int main () {
while ( cin >> m >> n >> k ) {
cout << age ( m ) << endl ;
}
return 0 ;
}
根据递推式子C(m,n)=C(m-1,n)+C(m-1,n-1),求组合数C(m,n)。注意递推的终止条件是C(m,1)=m;以及一些m和n取值的一些特殊情况,如m < 0或n < 0或m < n时,C(m,n)值为0,m和n相等时,C(m,n)=1等。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数m和一个正整数n。
输出
输出组合数C(m,n)。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std ;
int C ( int m , int n ) {
if ( n == 1 ) return m ;
if ( m < 0 || n < 0 || m < n ) return 0 ;
if ( m == n ) return 1 ;
return C ( m - 1 , n ) + C ( m - 1 , n - 1 );
}
int main () {
int t ; cin >> t ;
while ( t -- ) {
int m , n ; cin >> m >> n ;
cout << C ( m , n ) << endl ;
}
return 0 ;
}
核反应堆中有α和β两种粒子。每秒钟内一个α粒子可以产生3个β粒子,而一个β粒子可以产生1个α粒子和2个β粒子。若在t=0时刻反应堆中有一个α粒子,求t时刻反应堆中分别有多少个α粒子和β粒子。
输入
输入有多个整数t,每个一行。
输出
输出t时刻反应堆里分别有多少个α粒子和β粒子。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace std ;
pair < int , int > qut ( int n ) {
if ( n == 0 ) return make_pair ( 1 , 0 );
int tempa = qut ( n - 1 ). first , tempb = qut ( n - 1 ). second ;
int a = tempb , b = 3 * tempa + 2 * tempb ;
return make_pair ( a , b );
}
int main () {
int t ;
while ( cin >> t ) {
cout << qut ( t ). first << " " << qut ( t ). second << endl ;
}
return 0 ;
}
插一句:这里用了pair数据类型,或许有同学并没有接触到…一般函数会返回1个值,有时候想返回两个或以上的时候可以试试自定义struct数据类型,再去定义一个struct的函数,不过c++自有一个pair可以用,还是挺方便的。
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:白色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
样例输入
1
2
3
4
5
6
7
8
9
10
11
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std ;
const int maxh = 25 ;
string mp [ maxh ];
int dx [ 4 ] = { - 1 , 0 , 1 , 0 }, dy [ 4 ] = { 0 , 1 , 0 , - 1 };
int w , h ;
int move ( int x , int y , int allstep ) {
for ( int i = 0 ; i < 4 ; i ++ ) {
int nx = x + dx [ i ], ny = y + dy [ i ];
if ( nx > - 1 && nx < h && ny >- 1 && ny < w && mp [ nx ][ ny ] == '.' ){
mp [ nx ][ ny ] = '#' ;
allstep = move ( nx , ny , allstep + 1 );
}
}
return allstep ;
}
int main () {
while ( cin >> w >> h && w != 0 && h != 0 ) {
int si , se ;
for ( int i = 0 ; i < h ; i ++ ) {
cin >> mp [ i ];
if ( mp [ i ]. find ( "@" ) != string :: npos ) {
si = i ; se = mp [ i ]. find ( "@" );
}
}
int steps = move ( si , se , 1 );
cout << steps << endl ;
}
return 0 ;
}
1 2 3 4 5 6 7
#############################
1 # | # | # | | #
#####—#####—#—#####—#
2 # # | # # # # #
#—#####—#####—#####—#
3 # | | # # # # #
#—#########—#####—#—#
4 # # | | | | # #
#############################
(图 1)
‘#’ = Wall
‘|’ = No wall
‘-’ = No wall
图1是一个城堡的地形图。请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。城堡被分割成m*n(m≤50,n≤50)个方块,每个方块可以有0~4面墙。
输入
程序从标准输入设备读入数据。第一行是两个整数,分别是南北向、东西向的方块数。在接下来的输入行里,每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙,1表示西墙,2表示北墙,4表示东墙,8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。
输出
城堡的房间数、城堡中最大房间所包括的方块数。
样例输入
1
2
3
4
5
6
4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std ;
const int N = 60 ;
int wall [ N ][ N ], fw [ N ][ N ];
int roomnum = 0 , sizea = 0 ;
void dfs ( int x , int y ) {
// 查找点(x,y)的信息
if ( fw [ x ][ y ]) return ;
sizea ++ ;
fw [ x ][ y ] = roomnum ;
if (( wall [ x ][ y ] & 1 ) == 0 ) dfs ( x , y - 1 );
if (( wall [ x ][ y ] & 2 ) == 0 ) dfs ( x - 1 , y );
if (( wall [ x ][ y ] & 4 ) == 0 ) dfs ( x , y + 1 );
if (( wall [ x ][ y ] & 8 ) == 0 ) dfs ( x + 1 , y );
}
int main () {
int h , w ; cin >> h >> w ;
for ( int i = 1 ; i <= h ; i ++ ){
for ( int j = 1 ; j <= w ; j ++ ){
cin >> wall [ i ][ j ];
}
}
int maxroom = 0 ;
for ( int i = 1 ; i <= h ; i ++ ) {
for ( int j = 1 ; j <= w ; j ++ ) {
if ( ! fw [ i ][ j ]) {
// (i,j)没被找过(新的area)
roomnum ++ ;
dfs ( i , j );
maxroom = max ( maxroom , sizea );
sizea = 0 ;
}
}
}
cout << roomnum << endl << maxroom << endl ;
return 0 ;
}
/*
2
1 4
8
*/
给出一个正整数a,要求分解成若干个正整数的乘积,即a = a1 * a2 * a3 * … * an,并且1 < a1 <= a2 <= a3 <= … <= an,问这样的分解的种数有多少。注意到a = a也是一种分解。
输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a (1 < a < 32768)。
输出
n行,每行输出对应一个输入。输出应是一个正整数,指明满足要求的分解的种数。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std ;
int ans = 0 ;
void dfs ( int tar , int now ) {
if ( tar != 1 ) {
for ( int i = now ; i <= tar ; i ++ )
if ( tar % i == 0 )
dfs ( tar / i , i );
}
else {
ans ++ ; return ;
}
}
int main () {
int t ; cin >> t ;
while ( t -- ) {
ans = 0 ;
int n ; cin >> n ;
if ( n == 2 ) {
cout << 1 << endl ;
continue ;
}
dfs ( n , 2 );
cout << ans << endl ;
}
return 0 ;
}
现在给你这样一个任务,要求找出具有下列性质数的个数(包含输入的正整数 n)。
先输入一个正整数 n(n <= 500),然后对此正整数按照如下方法进行处理:
不作任何处理; 在它的左边拼接一个正整数,但该正整数不能超过原数的一半或者是上一个被拼接数的一半; 加上数后,继续按此规则进行处理,直到不能再加正整数为止。 输入
一个正整数n。
输出
一个正整数,表示具有该性质数的个数。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std ;
int fx [ 1010 ];
int f ( int n ) {
if ( n == 1 ) return 1 ;
if ( fx [ n ]) return fx [ n ];
int cnt = 0 ;
for ( int i = 1 ; i <= n / 2 ; i ++ )
cnt += f ( i );
return fx [ n ] = cnt + 1 ;
}
int main () {
int n ;
cin >> n ;
cout << f ( n ) << endl ;
return 0 ;
}
有一只快乐的蠕虫居住在一个m×n大小的网格中。在网格的某些位置放置了k块石头。网格中的每个位置要么是空的,要么放置了一块石头。当蠕虫睡觉时,它在水平方向或垂直方向上躺着,把身体尽可能伸展开来。蠕虫的身躯既不能进入到放有石块的方格中,也不能伸出网格外。而且蠕虫的长度不会短于2个方格的大小。
本题的任务是给定网格,要计算蠕虫可以在多少个不同的位置躺下睡觉。
输入
输入文件的第1行是一个整数t,1<=t<=11,表示测试数据的个数。每个测试数据的第1行为3个整数:m,n和k(0<=m,n,k<=200000),接下来有k行,每行为2个整数,描述了一块石头的位置(行和列,最左上角位置为(1,1))。
输出
对每个测试数据,输出占一行,为一个整数,表示蠕虫可以躺着睡觉的不同位置的数目。
样例输入
1
2
3
4
5
6
7
8
1
5 5 6
1 5
2 3
2 4
4 2
4 3
5 1
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e5 + 50 ;
int n , m , k ;
struct node {
int x , y ;
node ( int x , int y ) : x ( x ), y ( y ) {}
};
bool cmp1 ( node a , node b ) {
if ( a . x == b . x )
return a . y < b . y ;
return a . x < b . x ;
}
bool cmp2 ( node a , node b ) {
if ( a . y == b . y )
return a . x < b . x ;
return a . y < b . y ;
}
vector < node > a ;
int ans = 0 ;
void search ( bool f ) {
for ( int i = 1 ; i < a . size (); i ++ ) {
int nx = a [ i ]. x , ny = a [ i ]. y ;
int px = a [ i - 1 ]. x , py = a [ i - 1 ]. y ;
if ( f ) {
if ( nx != px ) continue ;
if ( ny - py > 2 ) ans ++ ;
}
else {
if ( ny != py ) continue ;
if ( nx - px > 2 ) ans ++ ;
}
}
}
void solve () {
cin >> m >> n >> k ;
ans = 0 ;
a . clear ();
for ( int i = 0 ; i < k ; i ++ ) {
int x , y ; cin >> x >> y ;
a . push_back ( node ( x , y ));
}
for ( int i = 0 ; i < m + 2 ; i ++ ) {
a . push_back ( node ( i , 0 ));
a . push_back ( node ( i , n + 1 ));
}
for ( int i = 0 ; i < n + 2 ; i ++ ) {
a . push_back ( node ( 0 , i ));
a . push_back ( node ( m + 1 , i ));
}
sort ( a . begin (), a . end (), cmp1 );
search ( true );
sort ( a . begin (), a . end (), cmp2 );
search ( false );
cout << ans << endl ;
}
int main () {
int t ; cin >> t ;
while ( t -- )
solve ();
return 0 ;
}
在美国数以百万计的报纸中,有一种单词游戏称为猜词。游戏的目标是猜谜,为了找出答案中缺少的字母,有必要对4个单词的字母顺序重新调整。在本题中,你的任务是编写程序实现对单词中的字母顺序重新调整。
输入
输入文件包含4部分:
(1) 一部字典,包含至少1个单词,至多100个单词,每个单词占一行;
(2) 字典后是一行字符串“XXXXXX”,表示字典结束;
(3) 一个或多个被打乱字母顺序的“单词”,每个单词占一行,你必须整理这些字母的顺序;
(4) 输入文件的最后一样为字符串“XXXXXX”,代表输入文件结束。
所有单词,包括字典中的单词和被打乱字母顺序的单词,都只包含小写英文字母,并且至少包含一个字母,至多包含6个字母。字典中的单词不一定是按顺序排列的,但保证字典中的单词是唯一的。
输出
对输入文件中每个被打乱字母顺序的单词w,按字母顺序输出字典中所有满足以下条件的单词的列表:通过调整单词w中的字母顺序,可以变成字典中的单词。列表中的每个单词占一行。如果列表为空(即单词w不能转换成字典中的任何一个单词),则输出一行字符串“NOT A VALID WORD”。以上两种情形都在列表后,输出一行包含6个星号字符的字符串,表示列表结束。
样例输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
tarp
given
score
refund
only
trap
work
earn
course
pepper
part
XXXXXX
resco
nfudre
aptr
sett
oresuc
XXXXXX
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
score
******
refund
******
part
tarp
trap
******
NOT A VALID WORD
******
course
******
给出m个字符串,要求输出重复n次的字符串有几个。
输入
先给定一个N,N≤100000,接着输入N个字符串。
输出
对于每组测试数据,输出若干行,每行两个正整数,第一个数表示重复的次数,第二个数表示在此重复次数下有几种不同的字符串。
样例输入
1
2
3
4
5
6
5
BBA
BBA
BEA
DEC
CCF
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e5 + 50 ;
int nx [ N ];
int main () {
int n ; cin >> n ;
map < string , int > sts ;
string st ;
while ( n -- ) {
cin >> st ;
if ( sts . find ( st ) != sts . end ()) {
map < string , int >:: const_iterator it = sts . find ( st );
int cnt = ( * it ). second ;
sts [ st ] = ++ cnt ;
}
else
sts . insert ( make_pair ( st , 1 ));
}
map < string , int >:: const_iterator it = sts . begin ();
for (; it != sts . end (); it ++ ) {
nx [( * it ). second ] ++ ;
}
for ( int i = 1 ; i <= sts . size (); i ++ ) {
if ( nx [ i ])
cout << i << " " << nx [ i ] << endl ;
}
return 0 ;
}
N个赌徒一起决定玩一个游戏:
游戏刚开始的时候,每个赌徒把赌注放在桌上并遮住,侍者要查看每个人的赌注并确保每个人的赌注都不一样。如果一个赌徒没钱了,则他要借一些筹码,因此他的赌注为负数。假定赌注都是整数。
最后赌徒们揭开盖子,出示他们的赌注。如果谁下的赌注是其他赌徒中某3个人下的赌注之和,则他是胜利者。如果有多于一个胜利者,则下的赌注最大的赌徒才是最终的胜利者。
例如,假定赌徒为:Tom、Bill、John、Roger和Bush,他们下的赌注分别为:2、3、5、7和12 。因此最终获胜的是Bush(并且没有其他人是胜利者),因为他下的赌注为12,而其他的人下的赌注之和也等于12:2+3+7=12。
输入
输入文件中包含了多组赌徒下的赌注。每组赌注的数据第1行是一个整数n,1<=n<=1000,代表赌徒的个数,然后是他们下的赌注,每个人的赌注占一行,这些赌注各不相同,并且范围是[-536870912,+536870911]。输入文件的最后一行为0,代表输入结束。
输出
对每组赌注,输出胜利者下的赌注,如果没有解,则输出“no solution”。
样例输入
1
2
3
4
5
6
7
8
9
10
11
12
13
5
2
3
5
7
12
5
2
16
64
256
1024
0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1050 ;
int n ;
int gbr [ maxn ];
void solve () {
for ( int i = 0 ; i < n ; i ++ ) {
cin >> gbr [ i ];
}
sort ( gbr , gbr + n );
for ( int pi = n - 1 ; pi >= 3 ; pi -- ) {
for ( int i = pi - 1 ; i >= 2 ; i -- ) {
for ( int j = i - 1 ; j >= 1 ; j -- ) {
for ( int k = j - 1 ; k >= 0 ; k -- ) {
int sum = gbr [ i ] + gbr [ j ] + gbr [ k ];
if ( sum == gbr [ pi ]) {
cout << gbr [ pi ] << " \n " ;
return ;
}
}
}
}
}
cout << "no solution \n " ;
}
int main () {
// int t;cin >> t;
// while (t--)
while ( cin >> n && n )
solve ();
return 0 ;
}
素数的定义:对于一个大于1的正整数,如果除了1和它本身没有其他的正约数了,那么这个数就称为素数。例如,2,11,67,89是素数,8,20,27不是素数。
半素数的定义:对于一个大于1的正整数,如果它可以被分解成2个素数的乘积,则称该数为半素数,例如6是一个半素数,而12不是。
你的任务是判断一个数是否是半素数。
输入
输入文件中有多个测试数据,每个测试数据包含一个整数N,2<=N<=1,000,000。
输出
对每个测试数据,如果N是半素数,则输出YES,否则输出NO。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 100 ;
bool isnp [ maxn ];
vector < int > primes ;
void Prime ( int n ) {
for ( int i = 2 ; i <= n ; i ++ ) {
if ( ! isnp [ i ])
primes . push_back ( i );
for ( int p : primes ) {
if ( p * i > n ) break ;
isnp [ p * i ] = true ;
if ( i % p == 0 )
break ;
}
}
}
int main () {
Prime ( maxn - 50 );
int n ;
while ( cin >> n ) {
bool f = false ;
for ( int i = 2 ; i * i <= n ; i ++ ) {
if ( n % i == 0 && ! isnp [ i ] && ! isnp [ n / i ]){
f = true ; break ;
}
}
f ? cout << "YES \n " : cout << "NO \n " ;
}
return 0 ;
}
当一根长度为L的细长金属棍子加热n度后,它会膨胀到一个新的长度L’=(1+n*C)*L,其中C为该金属的热膨胀系数。
当一根细长的金属棍子固定在两堵墙之间,然后加热,则棍子会变成圆弓形,棍子的原始位置为该圆弓形的弦,如图所示。

图 膨胀的金属棍子(上为膨胀前,下为膨胀后)
你的任务是计算棍子中心的偏离距离。
输入
输入文件包含多个测试数据,每个测试数据占一行。每个测试数据包含3个非负整数:棍子的初始长度,单位为毫米;加热前后的温差,单位为度;该金属的热膨胀系数。输入数据保证膨胀的长度不超过棍子本身长度的一半。输入文件的最后一行为3个负数,代表输入结束,该测试数据不需处理。
输出
对每个测试数据,输出金属棍子中心加热后偏离的距离,单位为毫米,保留小数点后3位有效数字。
样例输入
1
2
3
4
1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1
样例输出
1
2
3
61.329
225.020
0.000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const double eps = 1e-12 ;
const double pi = 3.1415926535 ;
int main () {
double l , t , c ;
while ( cin >> l >> t >> c ) {
if ( l < 0 && t < 0 && c < 0 ) break ;
double nl = ( 1.0 + t * c ) * l ;
double dr = pi , dl = 0.0 ;
while ( 1 ) {
double mid = ( dr + dl ) / 2 ;
double r = l / ( sin ( mid / 2 ) * 2 );
if ( dr - dl < eps ) {
double ans = r - r * cos ( mid / 2.0 );
printf ( "%.3lf \n " , ans );
break ;
}
double bar = mid * r ;
if ( bar > nl ) dr = mid ;
else dl = mid ;
}
}
return 0 ;
}
奶牛的居民决定举办一场编程区域赛。裁判委员会自告奋勇并宣称要举办有史以来最公正的比赛。队员们的电脑采用“星型”拓扑结构互连(也就是说要把所有电脑都连在一个中央集线器上)。为了让比赛尽可能公正,裁判委员会的头头们决定:将比赛队员们平均地安置在集线器周围,距离集线器有一个相同的距离。
裁判委员会为了采买网络电缆,联系了一家当地的网络方案提供商,要求他们提供一些登等长的电缆。这些电缆应越长越好,从而使得队员们与其他队员的距离越大。
这家公司的电缆工来办这件事。他知道仓库里每个电缆的长度(精确到厘米)。他每次切割电缆时的精度也是厘米。但他现在不知切多少,所以完全茫然中。
你要写个程序计算出一条电缆最多多长使之可以提供一定能够数目的电缆,帮着这位电缆工完成任务。
输入
第一行是两个整数N和K,N(1<=N<=10000)是仓库里的电缆数,K(1<=K<=10000)是所需电缆数。接下来的N行每一行一个数,表示电缆的长度(单位是米)。电缆长度最小为1米,最大为100千米。每个表示长度的数均表示为带两位小数的浮点数(即精确到厘米)。
输出
所需的电缆一条最长有多少米(精确到厘米,即保留小数点两位)。如果不能提供K条大于等于1厘米的等长电缆就输出“0.00”。
样例输入
1
2
3
4
5
4 11
8.02
7.43
4.57
5.39
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 10050 ;
int len [ maxn ];
int n , k ;
int cnt ( int l ) {
int ret = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
ret += len [ i ] / l ;
}
return ret ;
}
int main () {
cin >> n >> k ;
int left = 1 , right = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
double ni ; cin >> ni ;
ni *= 100 ;
right = max ( right , ( int ) ni );
len [ i ] = ( int ) ni ;
}
if ( cnt ( 1 ) < k ) {
cout << "0.00 \n " ;
return 0 ;
}
int ans = 0 ;
while ( left <= right ) {
int mid = ( left + right ) / 2 ;
if ( cnt ( mid ) < k ) right = mid - 1 ;
else {
ans = mid ;
left = mid + 1 ;
}
}
printf ( "%.2lf" , 1.0 * ans / 100 );
return 0 ;
}
你刚刚从奶牛搬到一个大城市里。这里的人说一种让人理解不能的外文方言。万幸,你有本字典可以帮助你理解。
输入
输入包含多达100,000个字典词条,然后是一个空行,然后是一条消息,这条消息包含多达100,000个单词。每个词条占一行,先是一个英语单词,然后是一个空格,然后是一个外文方言词。一个方言词在字典中出现不超过一次。消息是一个外文方言词序列,一个词占一行。每个词是一个最长为10的小写字母序列。
输出
将消息的外文词翻译成英语,一个词一行。查不到的词应该翻译成“eh”。
样例输入
1
2
3
4
5
6
7
8
9
dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay
atcay
ittenkay
oopslay
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 10050 ;
map < string , string > mp ;
int main () {
string s1 , s2 ;
while ( 1 ) {
char t = getchar ();
if ( t == '\n' ) break ;
cin >> s1 >> s2 ;
s1 . insert ( s1 . begin (), t );
mp . insert ( make_pair ( s2 , s1 ));
cin . get ();
}
string word ;
while ( cin >> word ) {
auto pos = mp . find ( word );
if ( pos != mp . end ()) {
cout << pos -> second << endl ;
}
else cout << "eh \n " ;
}
return 0 ;
}
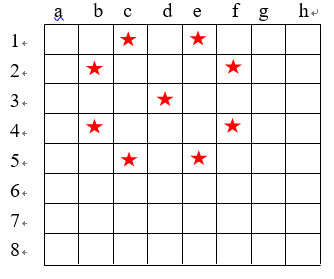
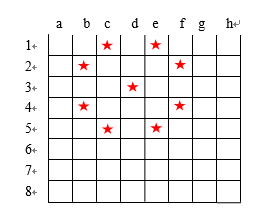
将夜空抽象成二维平面,每个星星一个(X,Y)坐标。这些点可以形成多少正方形?
输入
多组输入。对于每组数据,第一行是n(1<=n<=1000)表示已知星星数,然后是n行,每行一个坐标值。坐标绝对值小于20000。n=0表示结束。
输出
对于每组数据输出形成正方形的个数。
样例输入
1
2
3
4
5
6
4
1 0
0 1
1 1
0 0
0
样例输出
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的左边的那个数或者右边的那个数。
输入
输入的第一行是一个整数N (1 < N <= 100),给出三角形的行数。下面的N行给出数字三角形。数字三角形上的数的范围都在0和100之间。
输出
输出最大的和。
样例输入
1
2
3
4
5
6
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 120 ;
ll number [ maxn ][ maxn ];
ll dp [ maxn ][ maxn ]; // 记录走到(i,j)点时最好的和
int main () {
int n ;
while ( cin >> n ) {
for ( int i = 1 ; i <= n ; i ++ )
for ( int j = 1 ; j <= i ; j ++ )
cin >> number [ i ][ j ];
for ( int i = 1 ; i < n ; i ++ )
dp [ n ][ i ] = number [ n ][ i ];
for ( int i = n ; i > 1 ; i -- ) {
for ( int j = 1 ; j <= i ; j ++ ) {
dp [ i - 1 ][ j ] = max ( dp [ i ][ j ], dp [ i ][ j + 1 ]) + number [ i - 1 ][ j ];
}
}
cout << dp [ 1 ][ 1 ] << endl ;
}
return 0 ;
}
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … <iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8)。
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
输入
输入有很多组,每组输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000。
输出
输出每组的最长上升子序列的长度。
样例输入
1
2
3
4
7
1 7 3 5 9 4 8
6
2 3 4 1 6 5
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<vector>
using namespace std ;
typedef long long ll ;
const int maxn = 1010 ;
int a [ maxn ];
// int dp[maxn];
int main () {
int n ;
while ( cin >> n ) {
for ( int i = 1 ; i <= n ; i ++ ) cin >> a [ i ];
vector < int > lmax ;
lmax . push_back ( a [ 1 ]);
for ( int i = 2 ; i <= n ; i ++ ) {
if ( a [ i ] > lmax . back ()) {
lmax . push_back ( a [ i ]);
}
else if ( a [ i ] < lmax . back ()) {
int l = 0 , r = lmax . size () - 1 ;
while ( l < r ) {
int md = ( l + r ) / 2 ;
if ( lmax [ md ] <= a [ i ]) l = md + 1 ;
else r = md ;
}
lmax [ l ] = a [ i ];
}
// for (int j = 0;j < lmax.size();j++)
// cout << lmax[j] << " ";
// cout << endl;
}
cout << lmax . size () << endl ;
}
return 0 ;
}
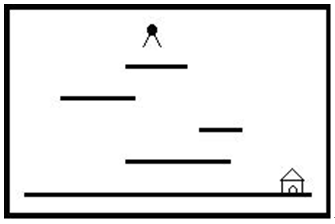
“Help Jimmy” 是在下图所示的场景上完成的游戏:
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到地面时可能的最早时间。
输入
第一行是测试数据的组数t(0 <= t <= 20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]和X2[i]表示平台左右端点的横坐标。1<= N <= 1000,-20000 <= X, X1[i], X2[i] <= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。
Jimmy 的大小和平台的厚度均忽略不计。如果Jimmy 恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保Jimmy一定能安全到达地面。
输出
对输入的每组测试数据,输出一个整数,Jimmy到地面时可能的最早时间。
样例输入
1
2
3
4
5
1
3 8 17 20
0 10 8
0 10 13
4 14 3
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 2e4 + 20 ;
struct PT {
int x1 , x2 , h ;
bool operator < ( const PT & P ) const {
return h > P . h ;
}
} pt [ maxn ];
int n , x , y , mx ;
int findnext ( int id , int x ) {
// 寻找x下的第一块板
for ( int i = id + 1 ; i <= n + 1 ; i ++ ) {
if ( pt [ i ]. x1 <= x && pt [ i ]. x2 >= x ) {
return i ;
}
}
return - 1 ;
}
int fun [ maxn ];
int dfs ( int id , int p , int from ) {
// cout << id << " " << p << " " << from << endl;
int lp = pt [ id ]. x1 , rp = pt [ id ]. x2 ;
// 当前是否到达终点
if ( id == n + 1 )
return 0 ;
int lenl = - 1 , lenr = - 1 ;
// 左走
int lpid = findnext ( id , lp );
if ( lpid != - 1 && pt [ id ]. h - pt [ lpid ]. h <= mx ) {
// 可走
lenl = dfs ( lpid , lp , id );
}
// 右走
int rpid = findnext ( id , rp );
if ( rpid != - 1 && pt [ id ]. h - pt [ rpid ]. h <= mx ) {
// 可走
lenr = dfs ( rpid , rp , id );
}
if ( lenl != - 1 && lenr != - 1 )
return fun [ id ] = min ( lenl + p - lp , lenr + rp - p );
else if ( lenl == - 1 )
return fun [ id ] = lenr + rp - p ;
else if ( lenr == - 1 )
return fun [ id ] = lenl + p - lp ;
else
return 0 ;
}
int main () {
int t ; cin >> t ;
while ( t -- ) {
cin >> n >> x >> y >> mx ;
pt [ 0 ]. x1 = x ; pt [ 0 ]. x2 = x ; pt [ 0 ]. h = y ;
for ( int i = 1 ; i <= n ; i ++ ) {
cin >> pt [ i ]. x1 >> pt [ i ]. x2 >> pt [ i ]. h ;
}
pt [ n + 1 ]. h = 0 ; pt [ n + 1 ]. x1 = - maxn ; pt [ n + 1 ]. x2 = maxn ;
sort ( pt , pt + n + 1 );
// 从高到低排列
dfs ( 0 , x , - 1 );
cout << y + fun [ 0 ] << endl ;
}
return 0 ;
}
我们称序列Z = < z1, z2, …, zk >是序列X = < x1, x2, …, xm >的子序列当且仅当存在严格上升的序列< i1, i2, …, ik >,使得对j = 1, 2, … ,k, 有xij = zj。比如Z = < a, b, f, c > 是X = < a, b,c, f, b, c >的子序列。
现在给出两个序列X和Y,你的任务是找到X和Y的最大公共子序列,也就是说要找到一个最长的序列Z,使得Z既是X的子序列也是Y的子序列。
输入
输入包括多组测试数据。每组数据包括一行,给出两个长度不超过200的字符串,表示两个序列。两个字符串之间由若干个空格隔开。
输出
输入包括多组测试数据。每组数据包括一行,给出两个长度不超过200的字符串,表示两个序列。两个字符串之间由若干个空格隔开。
样例输入
1
2
3
abcfbc abfcab
programming contest
abcd mnp
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std ;
const int maxn = 220 ;
int dp [ maxn ][ maxn ];
int main () {
ios :: sync_with_stdio ( false );
cin . tie ( 0 );
cout . tie ( 0 );
string s , t ;
while ( cin >> s >> t ) {
s = " " + s ; t = " " + t ;
memset ( dp , 0 , sizeof ( dp ));
for ( int i = 1 ; i < s . size (); i ++ ) {
for ( int j = 1 ; j < t . size (); j ++ ) {
if ( s [ i ] == t [ j ])
dp [ i ][ j ] = dp [ i - 1 ][ j - 1 ] + 1 ;
else
dp [ i ][ j ] = max ( dp [ i - 1 ][ j ], dp [ i ][ j - 1 ]);
}
}
cout << dp [ s . size () - 1 ][ t . size () - 1 ] << endl ;
}
return 0 ;
}
在遥远的国家佛罗布尼亚,嫌犯是否有罪,须由陪审团决定。陪审团是由法官从公众中挑选的。先随机挑选n个人作为陪审团的候选人,然后再从这n个人中选m人组成陪审团。选m人的办法是:
控方和辩方会根据对候选人的喜欢程度,给所有候选人打分,分值从0到20。为了公平起见,法官选出陪审团的原则是:选出的m个人,必须满足辩方总分和控方总分的差的绝对值最小。如果有多种选择方案的辩方总分和控方总分的之差的绝对值相同,那么选辩控双方总分之和最大的方案即可。最终选出的方案称为陪审团方案。
输入
输入包含多组数据。每组数据的第一行是两个整数n和m,n是候选人数目,m是陪审团人数。注意,1<=n<=200, 1<=m<=20而且m<=n。接下来的n行,每行表示一个候选人的信息,它包含2个整数,先后是控方和辩方对该候选人的打分。候选人按出现的先后从1开始编号。两组有效数据之间以空行分隔。最后一组数据n=m=0。
输出
对每组数据,先输出一行,表示答案所属的组号, 如 ‘Jury #1’, ‘Jury #2’, 等。接下来的一行要象例子那样输出陪审团的控方总分和辩方总分。再下来一行要以升序输出陪审团里每个成员的编号,两个成员编号之间用空格分隔。每组输出数据须以一个空行结束。
样例输入
1
2
3
4
5
6
4 2
1 2
2 3
4 1
6 2
0 0
样例输出
1
2
3
Jury #1
Best jury has value 6 for prosecution and value 4 for defence:
2 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
using namespace std ;
const int N = 205 ;
const int inf = 0x3f ;
int dp [ N ][ 25 ][ 4 * N ], a [ N ], b [ N ];
vector < int > mark ;
int main ()
{
int n , m , T = 1 ;
while ( cin >> n >> m && n ) {
mark . clear ();
memset ( dp , - inf , sizeof ( dp ));
dp [ 0 ][ 0 ][ 400 ] = 0 ;
for ( int i = 1 ; i <= n ; i ++ ) {
cin >> a [ i ] >> b [ i ];
}
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 0 ; j <= m ; j ++ ) {
for ( int k = 0 ; k <= 800 ; k ++ ) {
dp [ i ][ j ][ k ] = dp [ i - 1 ][ j ][ k ];
int tt = k - a [ i ] + b [ i ];
if ( tt < 0 || tt >= 800 )
continue ;
if ( j == 0 )
continue ;
dp [ i ][ j ][ k ] = max ( dp [ i ][ j ][ k ], dp [ i - 1 ][ j - 1 ][ tt ] + a [ i ] + b [ i ]);
}
}
}
int t = 0 ;
while ( dp [ n ][ m ][ t + 400 ] < 0 && dp [ n ][ m ][ - t + 400 ] < 0 ) t ++ ;
if ( dp [ n ][ m ][ t + 400 ] > dp [ n ][ m ][ - t + 400 ]) t += 400 ;
else t = 400 - t ;
int nn = n , mm = m , cnt = 0 ;
while ( mm ) {
if ( dp [ nn ][ mm ][ t ] == dp [ nn - 1 ][ mm ][ t ]) {
nn -- ;
}
else {
mark . push_back ( nn );
t -= a [ nn ] - b [ nn ];
nn -- ; mm -- ;
cnt ++ ;
}
}
int sum1 = 0 , sum2 = 0 ;
for ( int i = 0 ; i < cnt ; i ++ ) {
sum1 += a [ mark [ i ]];
sum2 += b [ mark [ i ]];
}
cout << "Jury #" << T ++ << " \n Best jury has value " << sum1 << " for prosecution and value " << sum2 << " for defence: \n " ;
for ( int i = cnt - 1 ; i >= 0 ; i -- )
cout << mark [ i ] << ' ' ;
cout << " \n\n " ;
}
return 0 ;
}
给定一个n个整数的集合:A={a1, a2,…, an},我们如下定义函数d(A):
$$
d(A)=\max\limits_{1\leq s_1\leq t_1\leq s_2\leq t_2\leq n}
\begin{Bmatrix}
\sum_{i=s_1}^{t_1}a_i+\sum_{j=s_2}^{t_2}a_j\
\end{Bmatrix}
$$
你的任务就是计算函数d(A)的函数值。
提示:对于样例,我们选择{2,2,3,-3,4} 和 {5},进行想加得到函数d(A)的函数值。
输入量大,建议使用scanf();
输入
输入包含 T(<=30)个样例,在输入的第一行即是整数T。每个样例包含两行,第一行是整数 n(2<=n<=50000),第二行包含了n个整数: a1, a2, …, an. (|ai| <= 10000)。
输出
对于每个输入样例,输出一行,即如上定义函数d(A)的函数值。
样例输入
1
2
3
1
10
1 -1 2 2 3 -3 4 -4 5 -5
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std ;
const int maxn = 2200 ;
int a [ maxn ];
int leftt [ maxn ], rightt [ maxn ];
int lmax [ maxn ], rmax [ maxn ];
int main () {
int t ; cin >> t ;
while ( t -- ) {
int n ; cin >> n ;
for ( int i = 1 ; i <= n ; i ++ )
cin >> a [ i ];
leftt [ 1 ] = a [ 1 ]; rightt [ n ] = a [ n ];
lmax [ 1 ] = a [ 1 ]; rmax [ n ] = a [ n ];
for ( int i = 2 ; i <= n ; i ++ ) {
leftt [ i ] = max ( leftt [ i - 1 ] + a [ i ], a [ i ]);
lmax [ i ] = max ( lmax [ i - 1 ], leftt [ i ]);
}
for ( int i = n - 1 ; i > 0 ; i -- ){
rightt [ i ] = max ( rightt [ i + 1 ] + a [ i ], a [ i ]);
rmax [ i ] = max ( rmax [ i + 1 ], rightt [ i ]);
}
int ans = a [ 1 ];
for ( int i = 2 ; i <= n ; i ++ )
ans = max ( ans , lmax [ i - 1 ] + rmax [ i ]);
cout << ans << endl ;
}
return 0 ;
}
给你一个二维矩阵,元素是整数,有正有负。一个子矩阵就是最小1*1最大包含这个矩阵本身的矩阵。一个矩阵的和就是矩阵中所有元素求和,最大子矩阵就是所有子矩阵中和最大的那个字矩阵。下面是一个例子:
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
最大子矩阵在左下角
9 2
-4 1
-1 8
和值是15。
输入
输入的第一行是整数N,即表示要输入一个N * N的整数矩阵。接下来是N^2 个整数,每个整数之间被空格或者空行分开,这些整数即为矩阵中的数,按照列优先的顺序排列,即第一行整数从左至右输入,第二行从左至右输入…. 第n行从左至右输入。N不会大于100,矩阵中的整数范围为 [-127,127]。
输出
输出最大矩阵的和。
样例输入
1
2
3
4
0 -2 -7 0 9 2 -6 2
-4 1 -4 1 -1 8 0 -2
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std ;
const int maxn = 120 ;
int rec [ maxn ][ maxn ];
int pre [ maxn ][ maxn ];
int dp [ maxn ][ maxn ];
int main () {
int n ; cin >> n ;
pre [ 0 ][ 0 ] = 0 ;
// 二维前缀和
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 1 ; j <= n ; j ++ ) {
cin >> rec [ i ][ j ];
pre [ i ][ j ] = pre [ i - 1 ][ j ] + pre [ i ][ j - 1 ] - pre [ i - 1 ][ j - 1 ] + rec [ i ][ j ];
}
}
// for (int i = 1;i <= n;i++) {
// for (int j = 1;j <= n;j++) {
// cout << pre[i][j] << " ";
// }
// cout << endl;
// }
int ans = - 200 ;
for ( int xi = 1 ; xi <= n ; xi ++ ) {
for ( int yi = 1 ; yi <= n ; yi ++ ) {
for ( int xj = xi ; xj <= n ; xj ++ ) {
for ( int yj = yi ; yj <= n ; yj ++ ) {
int sum = pre [ xj ][ yj ] - pre [ xi - 1 ][ yj ] - pre [ xj ][ yi - 1 ] + pre [ xi - 1 ][ yi - 1 ];
ans = max ( ans , sum );
}
}
}
}
cout << ans << endl ;
return 0 ;
}
将整数n分成k份,且每份不能为空,任意两种分法不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5;1,5,1;5,1,1;
问有多少种不同的分法。
输入
每组数据由一行上的2个整数n,k构成(6<n≤200,2≤k≤6)。
输出
对每组测试数据,输出不同的分法整数。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
#define AUTHOR "DODOLA"
using namespace std ;
typedef long long ll ;
const int maxn = 220 ;
ll dp [ maxn ][ maxn ]; // i个小球放入j个盒子没有空盒的方法数
int main () {
int n , k ;
cin >> n >> k ;
for ( int i = 1 ; i <= n ; i ++ ) {
dp [ i ][ 1 ] = 1 ; dp [ i ][ 0 ] = 1 ;
}
for ( int i = 2 ; i <= n ; i ++ ) {
for ( int j = 2 ; j <= k ; j ++ ) {
if ( i > j )
dp [ i ][ j ] = dp [ i - 1 ][ j - 1 ] + dp [ i - j ][ j ];
else
dp [ i ][ j ] = dp [ i - 1 ][ j - 1 ];
}
}
cout << dp [ n ][ k ] << endl ;
return 0 ;
}
农夫约翰的农场在最近的一场暴风雨中被水淹没。但保险公司仅根据他得农场中最大的“湖泊”的大小赔偿一个数额。
农场可表示为N行M列的长方形网格,(1≤N≤100,1≤M≤100)。网格中的每个单元或是干的或是被淹没的,且恰有K个单元被水淹没,(1≤K≤N*M)。正如人们所希望的,湖泊是一个中间单元,它与其他的单元共享一条长边(不是角落)。任何与中间单元共享一条长边或者与连通单元共享一条长边的单元是一个连通单元,是湖泊的一部分。
输入
有多组数据。每组的第1行有3个整数N,M和K。第2行到第K+1行,是整数R和C,表示被淹没的位置。
输出
对每组测试数据,输出有最大湖泊的单元的数目。
样例输入
1
2
3
4
5
6
3 4 5
3 2
2 2
3 1
2 3
1 1
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 150 ;
int n , m , k ;
bool fd [ maxn ][ maxn ];
int mv [ 4 ][ 2 ] = { { 1 , 0 }, { - 1 , 0 }, { 0 , 1 }, { 0 , - 1 } };
int ans ;
int dfs ( int r , int c ) {
if ( r < 1 || r > n || c < 1 || c > m || ! fd [ r ][ c ]) return 0 ;
fd [ r ][ c ] = false ;
int ret = 1 ;
for ( int i = 0 ; i < 4 ; i ++ ) {
ret += dfs ( r + mv [ i ][ 0 ], c + mv [ i ][ 1 ]);
}
return ret ;
}
void solve () {
fill ( fd [ 0 ], fd [ 0 ] + maxn * maxn , false );
ans = 0 ;
for ( int ki = 0 ; ki < k ; ki ++ ) {
int r , c ; cin >> r >> c ;
fd [ r ][ c ] = true ;
}
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 1 ; j <= m ; j ++ ) {
if ( fd [ i ][ j ]) {
ans = max ( ans , dfs ( i , j ));
}
}
}
cout << ans << " \n " ;
}
int main () {
while ( cin >> n >> m >> k )
solve ();
return 0 ;
}
/*
0 1 0 0 0
0 0 1 1 0
0 1 1 0 0
*/
当无线电台在一个非常大的区域上传播信号时,为了每个接收器都能得到较强信号,使用转发器转发信号。然而,需要仔细地选择每个转发器使用的频道,以使附近的转发器不彼此干扰。如果邻近的转发器使用不同的频道,条件就得到满足。
因为无线电波的频谱是宝贵的资源,转发器所需频道的数量应减到最少。编程任务:读取转发器网络的描述信息,并计算出所需频道的最小使用量。
输入
输入包含许多转发器网络图。每幅图的第一行是转发器数目(1~26)。转发器用连续的大写字母表示,从A开始。例如,10个转发器的名称分别是A,B,C,…,I和J。当转发器的个数是0时,表示输入结束。
转发器数目之后,是其邻近关系的列表。每行的格式为
A:BCDH
表示转发器B、C、D和H与转发器A邻近。第一行描述与转发器A邻近的,第二行描述与B邻近的,直到描述完所有的转发器。如果某个转发器不与其他转发器相邻,它的形式为
A:
转发器依字母顺序列出。
注意:相邻是对称的关系;如果A与B相邻,那么B与A也相邻。因为转发器位于水平面内,由相邻的转发器构成的网络图没有相交的线。
输出
对于每幅图(除了最后一个没有转发器),输出一行,是转发器不互相干扰所需的最少频道数。输出格式参考样例输出。注意:频道数为1的话,“channel”为单数。
样例输入
1
2
3
4
5
6
7
8
9
2
A:
B:
4
A:BC
B:ACD
C:ABD
D:BC
0
样例输出
1
2
1 channel needed.
3 channels needed.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std ;
typedef long long ll ;
const int maxn = 120 ;
bool fd [ maxn ][ maxn ];
int ind [ 30 ], t ;
bool dfs ( int from , int clr ) {
// 从from着色
for ( int i = 0 ; i < clr ; i ++ ) {
bool f = true ; ind [ from ] = i ;
for ( int j = 0 ; j < from ; j ++ ) {
if ( ind [ j ] == i && fd [ from ][ j ]) {
f = false ;
break ;
}
}
if ( f && ( from == t - 1 || dfs ( from + 1 , clr )))
return true ;
}
return false ;
}
int main () {
while ( cin >> t ) {
cin . get ();
if ( t == 0 ) break ;
memset ( fd , 0 , sizeof ( fd ));
memset ( ind , 0 , sizeof ( ind ));
bool f = true ;
for ( int i = 0 ; i < t ; i ++ ) {
string msg ; cin >> msg ;
if ( msg . size () == 2 )
continue ;
f = false ;
int pid = msg [ 0 ] - 'A' ;
for ( int j = 2 ; j < msg . size (); j ++ ) {
fd [ pid ][ msg [ j ] - 'A' ] = true ;
fd [ msg [ j ] - 'A' ][ pid ] = true ;
}
}
if ( f )
cout << "1 channel needed. \n " ;
else if ( dfs ( 1 , 2 ))
cout << "2 channels needed. \n " ;
else if ( dfs ( 1 , 3 ))
cout << "3 channels needed. \n " ;
else
cout << "4 channels needed. \n " ;
}
return 0 ;
}
你的一个朋友正在研究骑士旅行问题(TKP)。在一个有n个方格的棋盘上,你得找到一条最短的封闭骑士旅行的路径,使能够遍历每个方格一次。他认为问题的最困难部分在于,对两个给定的方格,确定骑士移动所需的最小步数。所以你帮助他编写一个程序,解决这个“困难的”部分。你的任务是:输入有两个方格a和b,确定骑士在最短路径上从a到b移动的次数。
国际象棋中的骑士在棋盘上可移动的范围如下图:
输入
输入包含一组或多组测试例。每个测试例一行,是两个方格,用空格隔开。棋盘上的一个方格用一个字符串表示,字母(a-h)表示列,数字(1-8)表示行。
输出
对每个测试例,输出一行:“To get from xx to yy takes n knight moves.”。
样例输入
1
2
3
4
5
6
7
8
e2 e4
a1 b2
b2 c3
a1 h8
a1 h7
h8 a1
b1 c3
f6 f6
样例输出
1
2
3
4
5
6
7
8
To get from e2 to e4 takes 2 knight moves.
To get from a1 to b2 takes 4 knight moves.
To get from b2 to c3 takes 2 knight moves.
To get from a1 to h8 takes 6 knight moves.
To get from a1 to h7 takes 5 knight moves.
To get from h8 to a1 takes 6 knight moves.
To get from b1 to c3 takes 1 knight moves.
To get from f6 to f6 takes 0 knight moves.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 150 ;
string fs , ts ;
int mv [ 8 ][ 2 ] = { { - 2 , - 1 }, { - 2 , 1 }, { - 1 , - 2 }, { - 1 , 2 }, { 1 , - 2 }, { 1 , 2 }, { 2 , - 1 }, { 2 , 1 } };
void bfs ( int x1 , int y1 , int x2 , int y2 ) {
if ( x1 == x2 && y1 == y2 ) {
cout << "To get from " << fs << " to " << ts << " takes 0 knight moves. \n " ;
return ;
}
int stp = 0 ;
queue < pair < int , int >> q ;
q . push ({ x1 , y1 });
while ( ! q . empty ()) {
queue < pair < int , int >> qs ;
while ( ! q . empty ()) {
auto [ x , y ] = q . front (); q . pop ();
for ( int i = 0 ; i < 8 ; i ++ ) {
int nx = x + mv [ i ][ 0 ], ny = y + mv [ i ][ 1 ];
if ( nx < 0 || nx >= 8 || ny < 0 || ny >= 8 ) continue ;
if ( nx == x2 && ny == y2 ) {
cout << "To get from " << fs << " to " << ts << " takes " << stp + 1 << " knight moves. \n " ;
return ;
}
qs . push ({ nx , ny });
}
}
stp ++ ;
q = qs ;
}
}
void solve () {
int x1 = fs [ 0 ] - 'a' , y1 = fs [ 1 ] - '1' , x2 = ts [ 0 ] - 'a' , y2 = ts [ 1 ] - '1' ;
bfs ( x1 , y1 , x2 , y2 );
}
int main () {
while ( cin >> fs >> ts )
solve ();
return 0 ;
}
病理学实验室的技术人员需要分析幻灯片的数字图像。幻灯片上有许多要分析的目标,由鼠标单击确定一个目标。目标边界的周长是一个有用的测量参数。编程任务:确定选中目标的在周长。
数字化的幻灯片是一个矩形的网格,里面有点’.’,表示空的地方;有大写字母‘X’,表示目标的一部分。简单网格如下所示
方格中的一个X是指一个完整的网络方形区域,包括其边界和目标本身。网格中心的X与其边界上8个方向的X都是相邻的。任何两个相邻的X,其网格方形区域在边界或者拐角处是重叠的,所以他们的网格方形区域是相邻的。
一个目标是由一系列相邻X的网格方形区域连接起来构成的。在网格1中,一个目标填充了全部网格;在网格2中有两个目标,其中一个目标只占左下角的一个网格方形区域,其余的X属于另一个目标。
技术人员总是能单击到一个X,以选中包含该X的目标,记录单击时的坐标。行列号是从左上角开始,从1开始编号的。在网格1中,技术人员可以单击行2和列2选择目标;在网格2中,单击行2和列3就可以选中较大目标,单击行4和列3就不能选中任何目标。
一个有用的统计参数是目标的周长。假定每个X的每条边上有一个方形的单元。在网格1中目标的周长是8(4个边,每个边上有2个方形的单元);在网格2中,较大目标的周长是18,如下图所示。
目标中不会包含任何完全封闭的孔,所以下面最左边的网格不会出现,应该是右边的网格样式。
输入
输入有多组网格。对每个网格,第一行是网格的行列数(rows,columns),鼠标单击的行列号(row,column),其整数范围都是1-20.接下来就是rows行,由字符‘.’和‘X’构成。
当一行是4个0时,标志输入结束。一行中的4个数字之间各有一个空格。网格数据的行之间没有空行。
输出
对每个网络输出一行,是选中目标的周长。
样例输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2 2 2 2
XX
XX
6 4 2 3
.XXX
.XXX
.XXX
...X
..X.
X...
5 6 1 3
.XXXX.
X....X
..XX.X
.X...X
..XXX.
0 0 0 0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
#define AUTHOR "DODOLA"
// #include<queue>
// #include<iostream>
// #include<string>
using namespace std ;
const int maxn = 250 ;
typedef long long ll ;
int r , c , x , y ;
vector < string > mp ( maxn );
int mv [ 8 ][ 2 ] = {
{ 1 , 0 },{ 0 , 1 },{ - 1 , 0 },{ 0 , - 1 },
{ 1 , 1 },{ 1 , - 1 },{ - 1 , - 1 },{ - 1 , 1 },
};
int ans ;
bool ck [ maxn ][ maxn ];
void dfs ( int px , int py ) {
// cout << px << " " << py << endl;
// cout << ans << endl;
if ( mp [ px ][ py ] != 'X' || ck [ px ][ py ]) return ;
ck [ px ][ py ] = true ;
for ( int j = 0 ; j < 4 ; j ++ ) {
int xj = px + mv [ j ][ 0 ], yj = py + mv [ j ][ 1 ];
if ( mp [ xj ][ yj ] != 'X' )
ans ++ ;
}
for ( int i = 0 ; i < 8 ; i ++ ) {
int xi = px + mv [ i ][ 0 ];
int yi = py + mv [ i ][ 1 ];
dfs ( xi , yi );
}
}
string s0 ( '.' , maxn - 1 );
void solve () {
ans = 0 ;
fill ( ck [ 0 ], ck [ 0 ] + sizeof ( ck ), false );
fill ( mp . begin (), mp . end (), s0 );
for ( int i = 1 ; i <= r ; i ++ ) {
cin >> mp [ i ];
mp [ i ] = " " + mp [ i ] + " " ;
}
dfs ( x , y );
cout << ans << " \n " ;
}
int main () {
mp [ 0 ] = s0 ;
while ( cin >> r >> c >> x >> y ) {
if ( ! r && ! c && ! x && ! y ) break ;
solve ();
}
return 0 ;
}
Somurolov先生是一个国际象棋高手,他声称在棋盘上将骑士棋子从一点移动到另外一点,没有人比他快,你敢挑战他吗?
你的任务是编程计算出将一个骑士棋子从一点移动到另外一点,最少需要移动的步数。显而易见,这样你就有赢得Somurolov先生的机会。国际象棋中的骑士在棋盘上可移动的范围如下图:
输入
首先输入测试样例的个数n。接下来是n组输入数据,每组测试数据由三行整数组成:第一行是棋盘的边长l (4 <= l <= 300),整个棋盘的面积也就是 ll;第二行和第三行分别是骑士棋子的初始位置和目标位置,表示为整数对形式{0, …, l-1} {0, …, l-1}。保证棋子的初始和目标位置是棋盘上的合法位置。
输出
对于每一个输入的测试样例,请你算出骑士从初始位置移动到目标位置最小移动步数。如果初始位置和目标位置相同,那么骑士移动的距离就是0。最后单独一行输出所求距离。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
#include <queue>
#include <cstring>
#define AUTHOR "DODOLA"
using namespace std ;
struct P {
int x ;
int y ;
int step ;
};
int mv [ 8 ][ 2 ] = {
{ 1 , 2 }, { 2 , 1 }, { - 1 , 2 }, { - 2 , 1 },
{ 1 , - 2 }, { 2 , - 1 }, { - 1 , - 2 }, { - 2 , - 1 }
};
int bfs ( int n , int x1 , int y1 , int x2 , int y2 )
{
if ( x1 == x2 && y1 == y2 )
{
return 0 ;
}
bool gnd [ n ][ n ];
queue < P > q ;
memset ( gnd , 0 , sizeof ( gnd ));
P start , node ;
start . x = x1 ;
start . y = y1 ;
start . step = 0 ;
q . push ( start );
while ( ! q . empty ()) {
int x0 , y0 , step ;
start = q . front ();
q . pop ();
x0 = start . x ;
y0 = start . y ;
step = start . step ;
for ( int j = 0 ; j < 8 ; j ++ ) {
int x3 = x0 + mv [ j ][ 0 ];
int y3 = y0 + mv [ j ][ 1 ];
if ( x3 == x2 && y3 == y2 )
return step + 1 ;
if ( x3 >= 0 && x3 < n && y3 >= 0 && y3 < n && ! gnd [ x3 ][ y3 ]) {
node . x = x3 ;
node . y = y3 ;
node . step = step + 1 ;
q . push ( node );
gnd [ x3 ][ y3 ] = 1 ;
}
}
}
return 0 ;
}
int main () {
int t ;
cin >> t ;
while ( t -- ) {
int x1 , y1 , x2 , y2 , n ;
cin >> n >> x1 >> y1 >> x2 >> y2 ;
cout << bfs ( n , x1 , y1 , x2 , y2 ) << endl ;
}
return 0 ;
}
给出一个整数n,编程求出一个非零整数m,使得m是n的倍数,并且m的十进制表示中只有1和0。给出的n不大于200并且肯定存在对应的m,m是十进制数并且不大于100位。
输入
输入包含多组测试数据。每组测试数据只有一个整数n (1 <= n <= 200)。整数0标志输入的结束。
输出
对于每个n输出对应的整数m,m的十进制表示不多于100位。如果对于一个n存在多个合法的m,你只需输出一个即可。
样例输入
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 10 ;
int n ;
bool ck ( int x ) {
while ( x ) {
if ( x % 10 == 0 || x % 10 == 1 ) {
x /= 10 ;
continue ;
}
else return false ;
}
return true ;
}
void solve () {
for ( int i = 1 ;; i ++ ) {
int m = i * n ;
bool f = ck ( m );
if ( f ) {
cout << m << endl ;
return ;
}
}
}
int main () {
while ( cin >> n ) {
if ( n == 0 ) break ;
solve ();
}
return 0 ;
}
有一个矩形的房间,房间铺着正方形的地砖。每个地砖被涂上红色或者黑色。初始时你站在房间里的某个黑色地砖上,你每次只能移动到相邻的四个地砖之一,即上下左右移动,并且你每次只能移动到黑色的地砖上,不能走到红色地砖。
编程计算出按照上述要求你能走到的黑色地砖的个数。
输入
输入包含多组测试数据。每组测试数据第一行包括2个整数W和H;W和H是房间的宽度和长度,分别表示为房间的x和y坐标轴。W和H不大于20。接下来是H行每行W个地砖的房间,每个地砖表示如下:
‘.’——黑色地砖
‘#’——红色地砖
‘@’ ——你在房间里的初始位置(房间只出现一次)。
输入的最后一行是两个整数0,不用处理。
输出
对每个测试样例,输出一行,即你能走到的黑色地砖的个数(包括你初始站在的黑色地砖)。
样例输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
0 0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <queue>
#include <cstring>
const int maxn = 120 ;
using namespace std ;
int r , c ;
char mp [ maxn ][ maxn ];
int mv [ 4 ][ 2 ] = {
{ 0 , 1 },{ 0 , - 1 },{ 1 , 0 },{ - 1 , 0 },
};
int ans ;
void dfs ( int x , int y ) {
if ( x < 0 || x == c || y < 0 || y == r ) return ;
if ( mp [ x ][ y ] == '#' ) return ;
ans ++ ;
mp [ x ][ y ] = '#' ;
for ( int i = 0 ; i < 4 ; i ++ ) {
int xi = x + mv [ i ][ 0 ];
int yi = y + mv [ i ][ 1 ];
dfs ( xi , yi );
}
}
void solve () {
ans = 0 ;
int px , py ;
for ( int i = 0 ; i < c ; i ++ ) {
for ( int j = 0 ; j < r ; j ++ ) {
cin >> mp [ i ][ j ];
if ( mp [ i ][ j ] == '@' ) {
px = i ; py = j ;
}
}
}
dfs ( px , py );
cout << ans << endl ;
}
int main () {
while ( cin >> r >> c ) {
if ( ! r && ! c ) break ;
solve ();
}
return 0 ;
}
George有一些长度相等的木棒,他随意的将这些木棒切成长度最多是50的小木棒。麻烦来了,他现在想将这些杂乱的小木棒恢复到原来的木棒,但是他忘记了原来到木棒的数量和长度。请你帮助他设计一个程序计算出原来木棒可能的最小长度,所有小木棒的长度均表示为大于0的整数。
输入
每组输入数据包括两行。第一行是George切后小木棒的个数,最多有64根小木棒;第二行是这些小木棒的长度,这些长度表示为空格分开的整数。输入样例以整数0表示结束。
输出
输出一行,即为原始木棒可能的最小长度。
样例输入
1
2
3
4
5
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
using namespace std ;
const int maxn = 80 ;
int n , a [ maxn ], maxv , tot , vis [ maxn ], k , len ;
bool cmp ( int a , int b ) {
return a > b ;
}
bool dfs ( int i , int rest , int p ) {
if ( i > k )
return 1 ;
int fail = 0 ;
for ( int x = p + 1 ; x <= n ; x ++ ) {
if ( ! vis [ x ]) {
if ( a [ x ] == a [ fail ]) continue ;
if ( rest > a [ x ]) {
vis [ x ] = 1 ;
bool w = dfs ( i , rest - a [ x ], x );
vis [ x ] = 0 ;
if ( ! w ) fail = x ;
if ( w ) return 1 ;
}
else if ( rest == a [ x ]) {
vis [ x ] = 1 ;
bool w = dfs ( i + 1 , len , 0 );
vis [ x ] = 0 ;
return w ;
}
if ( p == 0 ) return 0 ;
}
}
return 0 ;
}
void solve () {
fill ( vis , vis + n + 5 , 0 );
maxv = tot = 0 ;
for ( int i = 1 ; i <= n ; i ++ ) {
cin >> a [ i ];
maxv = max ( maxv , a [ i ]);
tot += a [ i ];
}
sort ( a + 1 , a + 1 + n , cmp );
for ( len = maxv ; len <= tot ; len ++ ) {
if ( tot % len == 0 ) {
k = tot / len ;
if ( dfs ( 1 , len , 0 )) {
cout << len << endl ;
break ;
}
}
}
}
int main () {
while ( cin >> n && n )
solve ();
return 0 ;
}
现有n根木棒,已知它们的长度和重量。要用一部木工机一根一根地加工这些木棒。该机器在加工过程中需要一定的准备时间,是用于清洗机器,调整工具和模板的。木工机需要的准备时间如下:
(1) 第一根木棒需要1min的准备时间;
(2) 在加工了一根长为l,重为w的木棒之后,接着加工一根长为l’(l≤l’),重为w’(w≤w’)的木棒是不需要任何准备时间的。否则需要一分钟的准备时间。
给定n根木棒,你要找到最少的准备时间。例如现在有长和重分别为(4,9),(5,2),(2,1),(3,5)和(1,4)的五根木棒,那么所需准备时间最少为2min,顺序为(1,4),(3,5),(4,9),(2,1),(5,2)。
输入
输入有多组测试例。输入数据的第一行是测试例的个数(T)。每个测试例两行:第一行是一个整数n(1≤n≤5000),表示有多少根木棒;第二行包括n*2个整数,表示l1,w1,l2,w2,l3,w3,…,ln,wn,全部不大于10000,其中li和wi表示第i根木棒的长度和重量。数据由一个或多个空格分隔。
输出
输出是以分钟为单位的最少准备时间,一行一个。
样例输入
1
2
3
4
5
6
7
3
5
4 9 5 2 2 1 3 5 1 4
3
2 2 1 1 2 2
3
1 3 2 2 3 1
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e5 + 50 ;
int n ;
bool ck [ maxn ];
void solve () {
cin >> n ;
fill ( ck , ck + 5050 , false );
vector < pair < int , int >> len ;
for ( int i = 0 ; i < n ; i ++ ) {
int l , w ; cin >> l >> w ;
len . push_back ( make_pair ( l , w ));
}
sort ( len . begin (), len . end ());
int cnt = 0 , ans = 0 ;
while ( cnt < n ) {
ans ++ ;
int ki = 0 ;
int li = 0 , wi = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
if ( ! ck [ i ]) {
ki = i ;
li = len [ i ]. first , wi = len [ i ]. second ;
ck [ i ] = true ;
cnt ++ ;
break ;
}
}
// cout << ki << " " << li << " " << wi << endl;
for ( int i = 0 ; i < n ; i ++ ) {
if ( ck [ i ]) continue ;
if ( li <= len [ i ]. first && wi <= len [ i ]. second ) {
ck [ i ] = true ;
cnt ++ ;
li = len [ i ]. first , wi = len [ i ]. second ;
}
}
}
cout << ans << endl ;
}
int main () {
int t ; cin >> t ;
while ( t -- )
solve ();
return 0 ;
}
一个工厂生产的产品形状都是长方体,高度都是h,主要有1x1,2x2,3x3,4x4,5x5,6x6等6种。这些产品在邮寄时被包装在一个6x6xh的长方体包裹中。由于邮费很贵,工厂希望减小每个订单的包裹数量以增加他们的利润。因此他们需要一个好的程序帮他们解决这个问题。你的任务就是设计这个程序。
输入
输入包括多组测试数据,每一行代表一个订单。每个订单里的一行包括六个整数,用空格隔开,从小到大分别为这6种产品的数量。6个0表示文件结束。
输出
针对每个订单输出一个整数,占一行,代表对应的订单所需的最小包裹数。没有多余的空行。
样例输入
1
2
3
0 0 4 0 0 1
7 5 1 0 0 0
0 0 0 0 0 0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// #include<bits/stdc++.h>
#include<iostream>
using namespace std ;
typedef long long ll ;
const int maxn = 2e5 + 50 ;
int n ;
int b1 , b2 , b3 , b4 , b5 , b6 ;
int l3 [ 4 ] = { 0 , 7 , 6 , 5 };
int l2 [ 4 ] = { 0 , 5 , 3 , 1 };
int l1 [ 9 ] = { 0 , 32 , 28 , 24 , 20 , 16 , 12 , 8 , 4 };
void solve () {
int ans = b6 + b5 + b4 + ( b3 + 3 ) / 4 ;
int n2 = 5 * b4 + l2 [ b3 % 4 ];;
if ( n2 >= b2 ) {
int n1 = b5 * ( 36 - 25 ) + ( n2 - b2 ) * 4 + l3 [ b3 % 4 ];
if ( n1 < b1 )
ans += ( b1 - n1 + 35 ) / 36 ;
}
else {
int m2 = b2 - n2 ;
ans += ( m2 + 8 ) / 9 ;
int n1 = b5 * ( 36 - 25 ) + l3 [ b3 % 4 ] + l1 [ m2 % 9 ];
if ( n1 < b1 )
ans += ( b1 - n1 + 35 ) / 36 ;
}
cout << ans << endl ;
}
int main () {
while ( cin >> b1 >> b2 >> b3 >> b4 >> b5 >> b6 && ( b1 || b2 || b3 || b4 || b5 || b6 ))
solve ();
}
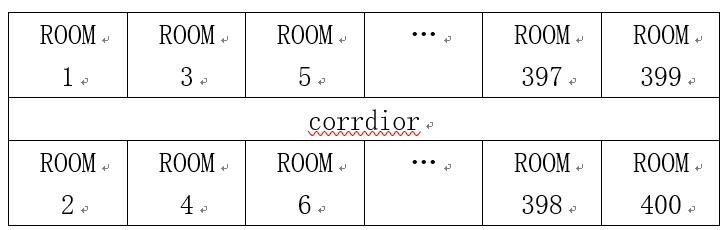
著名的ACM(Advanced Computer Maker)公司租用了一层有400个房间的办公楼,结构如下。
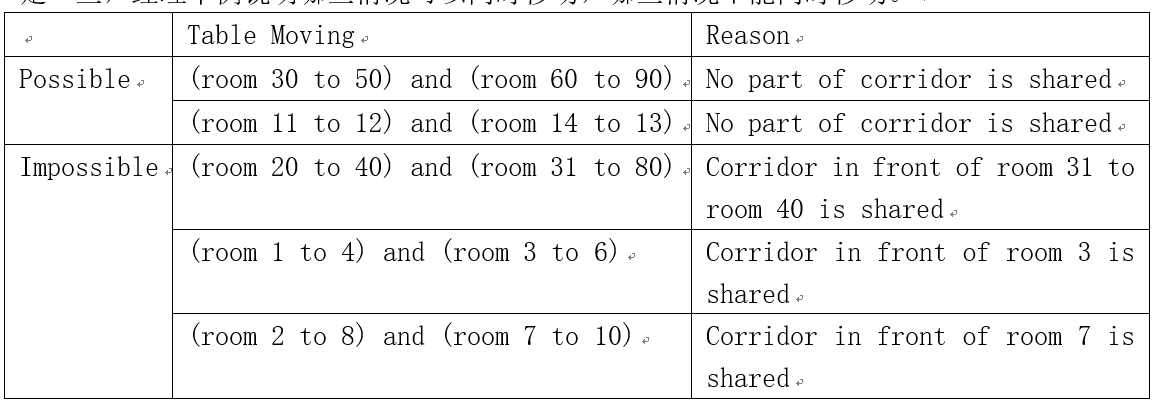
这层楼沿着走廊南北向的两边各有200个房间。最近,公司要做一次装修,需要在各个办公室之间搬运办公桌。由于走廊狭窄,办公桌都很大,走廊里一次只能通过一张办公桌。必须制定计划提高搬运效率。经理制定如下计划:一张办公桌从一个房间移动到另一个房间最多用十分钟。当从房间i移动一张办公桌到房间j,两个办公室之间的走廊都会被占用。所以,每10分钟内,只要不是同一段走廊,都可以在房间之间移动办公桌。为了说得更清楚一些,经理举例说明哪些情况可以同时移动,哪些情况不能同时移动。
每个房间,只有一张办公桌进出。现在,经理想找到一种方案,使移动桌子的事情尽快完成。请编写程序解决经理的难题。
输入
输入数据有T组测试例,在第一行给出测试例个数(T)。每个测试例的第一行是一个整数N(1≤N≤200),表示要搬运办公桌的次数。接下来N行,每行两个正整数s和t,表示一张桌子,是从房间号码s移到房间号码t。有多组输入数据,输入第一行为一个表示输入数据总数的整数N,然后是N组输入数据。
输出
每组输入都有一行的输出数据,为一整数T,表示完成任务所花费的最少时间。
样例输入
1
2
3
4
5
6
7
8
9
2
4
10 20
30 40
50 60
70 80
2
1 3
2 200
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// #include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std ;
typedef long long ll ;
const int maxn = 2e5 + 50 ;
int n ;
void solve () {
cin >> n ;
int pass [ 220 ] = {};
for ( int i = 1 ; i <= n ; i ++ ) {
int x , y ; cin >> x >> y ;
x = ( x + 1 ) / 2 ;
y = ( y + 1 ) / 2 ;
if ( x > y ) {
x = x ^ y ; y = x ^ y ; x = x ^ y ;
}
for ( int j = x ; j <= y ; j ++ ) {
pass [ j ] ++ ;
}
}
int ans = * max_element ( pass + 1 , pass + 201 );
cout << 10 * ans << endl ;
}
int main () {
int t ; cin >> t ;
while ( t -- )
solve ();
}
随着大量的基因组DNA序列数据被获得,它对于了解基因越来越重要(基因组DNA的一部分,是负责蛋白质合成的)。众所周知,在基因组序列中,由于存在垃圾的DNA中断基因的编码区,真核生物(相对于原核生物)的基因链更加复杂。也就是说,一个基因被分成几个编码片段(称为外显子)。虽然在蛋白质的合成过程中,外显子的顺序是固定的,但是外显子的数量和长度可以是任意的。
大多数基因识别算法分为两步:第一步,寻找可能的外显子;第二步,通过寻找一条拥有尽可能多的外显子的基因链,尽可能大地拼接一个基因。这条链必须遵循外显子出现在基因组序列中的顺序。外显子i在外显子j的前面的条件是i的末尾必须在j开头的前面。
本题的目标是,给定一组可能的外显子,找出一条拥有尽可能多的外显子链,拼接成一个基因。
输入
给出几组输入实例。每个实例的开头是基因组序列中可能的外显子数n(0 < n < 1000)。接着的n行,每行是一对整数,表示外显子在基因组序列中的起始和结束位置。假设基因组序列最长为50000。当一行是0时,表示输入结束。
输出
对于每个实例,找出最可能多的外显子链,输出链中的外显子,并占一行。假如有多条链,但外显子数相同,那么可以输出其中任意一条。
样例输入
1
2
3
4
5
6
7
8
6
340 500
220 470
100 300
880 943
525 556
612 776
0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 2e5 + 50 ;
struct node {
int x ; int y ;
int i ;
bool operator < ( const node & p ) const {
return x < p . x ;
}
} wxz [ maxn ];
int n ;
void solve () {
for ( int i = 1 ; i <= n ; i ++ ) {
cin >> wxz [ i ]. x >> wxz [ i ]. y ;
wxz [ i ]. i = i ;
}
sort ( wxz + 1 , wxz + 1 + n );
vector < node > ans ;
ans . push_back ( wxz [ 1 ]);
for ( int i = 2 ; i <= n ; i ++ ) {
struct node ni = ans . back ();
if ( ni . y > wxz [ i ]. y ) {
ans . pop_back (); ans . push_back ( wxz [ i ]);
}
else if ( ni . y < wxz [ i ]. x ) {
ans . push_back ( wxz [ i ]);
}
}
for ( int i = 0 ; i < ans . size (); i ++ ) {
cout << ans [ i ]. i << " " ;
}
cout << '\n' ;
}
int main () {
while ( cin >> n && n )
solve ();
}
多纳先生是ACM(Agent on Computing of Mathematics,计算数学代理商)大型计算机的管理员。该代理商为一些公司承担在大型计算机上的计算工作,完成工作后获得报酬,因此大型计算机对这个代理商来说太重要了。多纳先生需要为这些在大型计算机上运行的作业安排顺序。一旦要运行某个作业,他就要检查运行该作业所需要的空闲资源。如果空闲资源足够的话,他就为该作业分配这些资源;否则就将该作业挂起,直至有足够的资源投入运行。
刚开始他并不熟悉这项工作,把事情搞得很乱。日积月累,他就胜任这项工作了。而且他还总结了一套规则:
(1)大型计算机有M个CPU和N大小的内存空间可供分配。
(2)对等待运行的作业有一个等待队列。可以假定这个队列足够长,能够存放所有等待运行的作业。
(3)假定作业Ji需要Ai个CPU和Bi的内存空间,在时间Ti到达等待队列,需要在时间Ui之前完成。成功运行后,代理商可以获得Vi()的报酬;如果能在规定的时间之前完成,则每小时还可以额外获得Wi()的奖金;如果工期拖延,则每小时赔偿Xi()。例如,假定一个作业的报酬是10,时限8小时,每拖欠一小时罚2。如果该作业在10小时完成,则代理商可以获得10-(10-8)*2=6。
(4)当一个作业开始后,就独占了分配给它的CPU和内存空间,不能同时再分配给其他作业。当该作业运行结束后,这些资源被释放。如果资源足够多,同时可以运行多个作业。
(5)为了最大限度地发挥大型计算机的计算能力,每个作业在开始运行后刚好一小时就完成。你可以假定每个作业的运行时间就是一小时。
(6)没有作业运行时,机器空闲,一直到一个作业进入作业等待队列。
(7)如果有多个作业进入作业等待队列,则报酬高的作业优先。可以假定这些作业的报酬都不相等。
(8)如果某个作业的空闲CPU或内存空间不能满足,它就是被挂起一小时,也不占用任何资源。一小时后,再次为该作业检查资源,而不需要考虑等待队列里的其他作业。如果资源仍不满足要求,那就继续挂起一小时,把资源分配给其他在等待队列里的作业。否则,该作业将独占CPU和存储空间并投入运行。
(9)当多个作业挂起时,采取先来先服务的原则。
使用这些规则,多纳先生把事情安排得井井有条。现在除了日常公务外,代理商要求他根据作业列表计算收入。给定某个时间F,计算出已经完成的作业和应该被完成的作业。对作业Ji,如果它的时限Ui>F并且仍未完成,就不需要统计收入。对已经完成的作业或Ui≤F的作业都要统计。如果工作没有完成,它不会给代理商带来报酬,但到这个时间F为止的罚款仍要计算。
他不会程序设计,又不想手工做,现在你帮助他解决这个问题。
输入
有多组测试例。每个测试例描述大型计算机的资源和作业列表,第一行是整数F(0≤F≤10000),表示时限。接下来的一行是三个整数M,N和L(M,N,L≥0),M是机器CPU的数量,N是存储空间的大小,L是作业等待队列中作业的数量。最多有10000个作业。
后面的L行是作业的信息。描述作业Ji的数据是7个整数:Ai,Bi,Ti,Ui,Vi,Wi,Xi。Ai和Bi(Ai,Bi≥0)指出了该作业对CPU和内存的需求。Ti和Ui表示作业的到达时间和时限(0≤Ti≤Ui)。Vi,Wi,Xi分别是工作的报酬、奖励和罚款。
一个空的测试例(F=0)表示输入结束,该测试点无需处理。
输出
根据作业列表计算总收入。对每个测试例,输出测试例编号,一个冒号,一个空格,然后是收入。
测试例之间有一个空行。
注意:对尚未投入运行的、且时限超过F的作业,不必统计。
样例输入
1
2
3
4
5
6
10
4 256 3
1 16 2 3 10 5 6
2 128 2 4 30 10 5
2 128 2 4 20 10 5
0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e5 + 20 ;
struct JOB {
int a , b , t , u , v , w , x ;
bool ok ;
JOB ( int a , int b , int t , int u , int v , int w , int x ) : a ( a ), b ( b ), t ( t ), u ( u ), v ( v ), w ( w ), x ( x ), ok ( false ) {}
bool operator < ( const JOB & N ) const {
if ( N . t == t )
return v > N . v ;
return t < N . t ;
}
};
int ind = 1 ;
int f ;
int m , n , l ;
int mi , ni ;
void solve () {
cin >> m >> n >> l ;
vector < JOB > tot ;
for ( int i = 0 ; i < l ; i ++ ) {
int a , b , t , u , v , w , x ;
cin >> a >> b >> t >> u >> v >> w >> x ;
tot . push_back ( JOB ( a , b , t , u , v , w , x ));
}
sort ( tot . begin (), tot . end ());
int ans = 0 ;
for ( int i = 1 ; i <= f ; i ++ ) {
mi = m ; ni = n ;
for ( int j = 0 ; j < l ; j ++ ) {
if ( tot [ j ]. t >= i )
break ;
if ( tot [ j ]. ok || mi < tot [ j ]. a || ni < tot [ j ]. b )
continue ;
tot [ j ]. ok = true ;
mi -= tot [ j ]. a ;
ni -= tot [ j ]. b ;
ans += tot [ j ]. v ;
if ( i > tot [ j ]. u )
ans -= ( i - tot [ j ]. u ) * tot [ j ]. x ;
else if ( i < tot [ j ]. u )
ans += ( tot [ j ]. u - i ) * tot [ j ]. w ;
}
}
for ( int i = 0 ; i < l ; i ++ ) {
if ( ! tot [ i ]. ok && tot [ i ]. u <= f )
ans -= ( f - tot [ i ]. u ) * tot [ i ]. x ;
}
printf ( "Case %d: %d \n\n " , ind , ans );
ind ++ ;
}
int main () {
while ( cin >> f && f )
solve ();
return 0 ;
}
一个整数区间[a,b] (a < b),是一个从a到b连续整数的集合。
现在给你n个整数区间,编程找出一个集合R,使得n个集合中的每个集合都有2个整数出现在R中,并且这个集合R包含的整数个数最少。
输入
输入有多组数据,每组第一行包含整数n(1 <= n <= 10000),表示整数区间的个数。接下来n行,每行包含两个整数a和b(0 <= a < b <= 10000, a < b)。
输出
输出符合条件的集合R中元素的个数。
样例输入
1
2
3
4
5
4
3 6
2 4
0 2
4 7
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e5 + 50 ;
int cnt [ maxn ];
int n ;
int ck [ maxn ];
bool hasi [ maxn ];
void solve () {
while ( cin >> n ) {
fill ( hasi , hasi + 10005 , false );
fill ( ck , ck + n + 5 , 0 );
fill ( cnt , cnt + 10005 , 0 );
if ( ! n ) return ;
vector < pair < int , int >> v ;
for ( int i = 0 ; i < n ; i ++ ) {
int a , b ;
cin >> a >> b ;
v . push_back ( make_pair ( a , b ));
for ( int j = a ; j <= b ; j ++ ) {
cnt [ j ] ++ ;
}
}
int ans = 0 ;
while ( true ) {
int mx = max_element ( cnt , cnt + 10005 ) - cnt ;
// cout << mx << endl;
if ( cnt [ mx ] == 0 ) break ;
hasi [ mx ] = true ;
ans ++ ;
fill ( cnt , cnt + 10005 , 0 );
for ( int i = 0 ; i < n ; i ++ ) {
if ( ck [ i ] == 2 ) continue ;
if ( v [ i ]. first <= mx && v [ i ]. second >= mx ) {
ck [ i ] ++ ;
}
if ( ck [ i ] == 2 ) continue ;
for ( int j = v [ i ]. first ; j <= v [ i ]. second ; j ++ ) {
if ( hasi [ j ])
continue ;
cnt [ j ] ++ ;
}
}
}
cout << ans << endl ;
}
}
int main () {
// int t;cin >> t;
// while (t--)
solve ();
return 0 ;
}
我们假设海岸线是一条无限直线:以海岸线为界,陆地和海洋被分开,在海边分布着很多小岛。现在,我们在海岸线上安装雷达,每个雷达有固定的通讯范围(以d为半径的圆形区域),这样,海边的小岛就可以被某个雷达信号覆盖。
这里我们使用笛卡尔坐标系,定义海岸线为x轴,x轴上方是海洋,下方是陆地。给出分布在海边每个小岛的坐标位置和雷达信号能覆盖的范围d,你的任务是计算出最小需要安装的雷达数目,使得这些雷达信号能覆盖到所有海边的小岛。每个小岛的坐标格式为(x,y)。
如下图所示,给出第一个输入样例的坐标表示,这样在(-2,0),(1,0)上分别安装雷达就可以覆盖所有的小岛(p点),所以我们只需要安装2个雷达。
输入
输入包含多组测试样例。每组测试第一行包含两个整数n(1<=n<=1000)和d,n表示小岛的数目,d表示雷达能覆盖的范围的半径。接下来n行,每行由整数x和y组成,表示n个小岛的坐标位置。每两组数据之间有一个空行。
输入0 0表示输入的结束。
输出
对于每一组输入,按照输出样例中的格式输出:包含输出序号和最少需要安装雷达的数目。如果找不到解决方案,即不能找到一种安装方案覆盖所有的小岛,输出”-1”。
样例输入
1
2
3
4
5
6
7
8
9
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
struct node {
double x , y ;
node ( double x , double y ) : x ( x ), y ( y ) {}
bool operator < ( const node & a ) const {
return y < a . y ;
}
};
int n ;
int d ;
int ind ;
void solve () {
ind = 1 ;
while ( cin >> n >> d ) {
if ( n == 0 && d == 0 ) return ;
bool f = true ;
vector < node > q ;
for ( int i = 0 ; i < n ; i ++ ) {
int x , y ; cin >> x >> y ;
if ( d < y )
f = false ;
if ( ! f ) continue ;
double ei = sqrt ( 1.0 * d * d - 1.0 * y * y );
q . push_back ( node { x - ei , x + ei });
}
if ( ! f ) {
printf ( "Case %d: -1 \n " , ind );
ind ++ ;
continue ;
}
sort ( q . begin (), q . end ());
int ans = 1 ;
double yi = q [ 0 ]. y ;
for ( int i = 1 ; i < q . size (); i ++ ) {
if ( q [ i ]. x <= yi ) {
continue ;
}
else {
ans ++ ;
yi = q [ i ]. y ;
}
}
printf ( "Case %d: %d \n " , ind , ans );
ind ++ ;
}
}
int main () {
// int t;cin >> t;
// while (t--)
solve ();
return 0 ;
}
周晓晓吃完中午饭后又觉得没吃饱,因此想要再去食堂买点饭,当她走进食堂发现已经有n个人排队了,她知道每个人买饭需要的时间。她想帮助大家尽快的买到饭,即让n个人的平均等待时间最小,周晓晓已经饿的无法想出办法,只想知道他们最小的平均等待时间是多少,你能帮助她吗?
输入
输入可能有多组,每组第一行为一个整数n。 第二行 n 个整数,第 i 个整数 Ti 表示第i个人的等待时间Ti。
输出
每组输出占一行,为每组最小的平均等待时间(输出结果精确到小数点后两位)。
样例输入
1
2
10
56 12 1 99 1000 234 33 55 99 812
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e5 + 20 ;
int a [ maxn ];
int n ;
void solve () {
for ( int i = 0 ; i < n ; i ++ ) cin >> a [ i ];
sort ( a , a + n );
int ans = 0 ;
int tmp = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
tmp += a [ i ];
ans += tmp ;
}
printf ( "%.2lf \n " , 1.0 * ans / n );
}
int main () {
while ( cin >> n )
solve ();
return 0 ;
}
周小小最近想为自己的图书室添置一个巨型书架,尽管它是如此的大,但它还是几乎瞬间就被各种各样的书塞满了。现在,只有书架的顶上还留有一点空间。
所有N(1<=N<=2000)把椅子都有一个确定的高度Hi(1<=Hi<=1000)。为了够到书架顶,周小小想像演杂技一般,将椅子一个一个的叠在一起,并上去把书架的空间补上。
显然,椅子叠的越多,就越不稳定,于是小小希望在够到书架顶的前提下,让椅子数量尽量少,作为聪明的你,一定能帮助他计算出这个最小数量吧。
输入
第1行: 2个用空格隔开的整数:N和B,表示有N把椅子和书架的高度;
第2行到N+1行: 第i+1行是1个整数:Hi,表示椅子的高度。
可能存在多组输入数据。
输出
输出1个整数,即最少要多少把椅子。(如果到不了顶端,输出-1)
样例输入
1
2
3
4
5
6
7
6 40
6
18
11
13
19
11
样例输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 2010 ;
int h [ maxn ];
int n , b ;
void solve () {
for ( int i = 0 ; i < n ; i ++ )
cin >> h [ i ];
sort ( h , h + n );
int sum = 0 , cnt = 0 ;
for ( int i = n - 1 ; i >= 0 ; i -- ) {
sum += h [ i ];
cnt ++ ;
if ( sum >= b ) {
cout << cnt << endl ;
return ;
}
}
cout << - 1 << endl ;
}
int main () {
while ( cin >> n >> b )
solve ();
return 0 ;
}